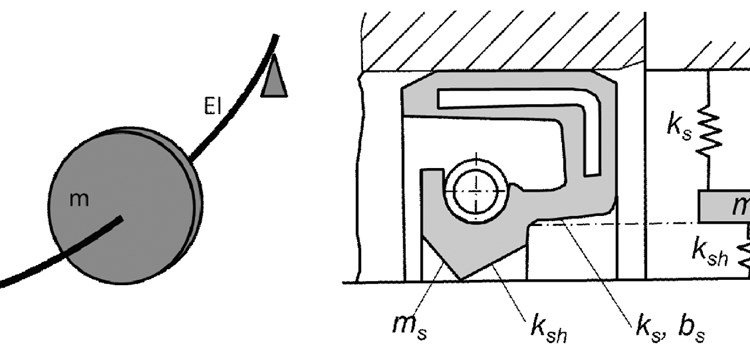
Lavalrotor (links) und Dichtung als Schwinger mit einem Freiheitsgrad (rechts) (Bild: HAW Hamburg)
31.10.2020 Technische Antriebe dichtungstechnisch optimieren
Theoretische Untersuchungen zur dynamischen Interaktion von Rotor und Wellendichtring
Die Ressourcenschonung in technischen Antrieben ist heute ein zentrales Thema. Auch durch Verbesserung bereits vorhandener Bauteile (Wellendichtringe), die ggf. auch nur temporär und bei Bedarf in den dynamischen Betrieb eingreifen, ist es möglich, Antriebsleistung einzusparen (Resonanzdurchfahrt) oder Beschädigungen (Beruhigung von Instabilitäten) zu verhindern. Diese Arbeit stellt theoretische Untersuchungen zur dynamischen Interaktion eines biegeelastischen Rotors mit einem Wellendichtring, vergleiche [1] und [2], in einer Arbeit zusammen.
Betrachtet werden sowohl die Resonanzdurchfahrt als auch das Problem der Instabilität infolge innerer Dämpfung, die bei hohen Drehzahlen auftreten kann. Beide Fragestellungen lassen sich an erstaunlich einfachen, wenn auch nicht trivialen Modellen untersuchen. Die Arbeit gliedert sich in drei Teile. Zunächst wird die den Untersuchungen zugrunde liegende Modellbildung erläutert, bevor die Ergebnisse numerischer Simulationen diskutiert werden. Abschließend werden die wesentlichen Erkenntnisse zusammengefasst.
Modellbildung Rotor mit Wellendichtring
Die Beschreibung des zu untersuchenden Problems basiert auf der Modellbildung des Lavalrotors [3] sowie auf der Abbildung eines elastomeren Wellendichtringes als diskretes Schwingungssystem nach [4]. Das Modell des Lavalrotors, dargestellt in
Bild 1, ist geeignet, um die Dynamik rotierender Maschinen für deren erste Eigenschwingungsform zu beschreiben. Es bildet die gesamte dynamische Masse (m) des Rotors auf eine in der Wellenmitte platzierte Scheibe ab, deren Schrägstellung ausgeschlossen wird. Effekte der äußeren Dämpfung werden durch einen Dämpfungsparameter (r) erfasst. Die Elastizität (s) resultiert aus der Biegesteifigkeit (EI) der Welle, die im vorliegenden Fall als isotrop und als über die Wellenlänge konstant angenommen wird. Innere Dämpfung wird nach [5] modelliert, wobei am Sitz der Scheibe wirkende diskrete Dämpfungskräfte angesetzt werden.

